Г.И. Шипов
Теория физического вакуума.
Философия и метанаука, научная и духовная мысль
Пространство событий.
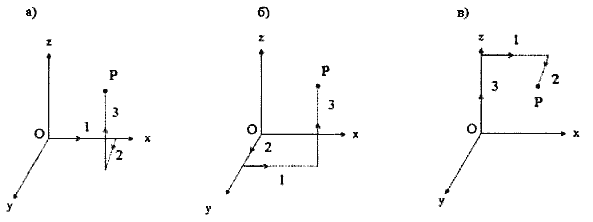
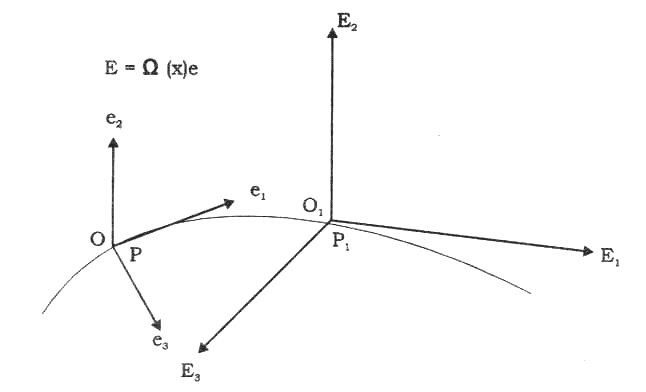
Западный метод познания природы начинается с того, что выбирается своеобразная "точка зрения" исследователя - система наблюдения или система отсчёта. В трёхмерном пространстве механики Ньютона система отсчёта представляет собой три взаимно перпендикулярных направленных отрезка прямой линии с общим началом О (см. рис. 1). Изучая, например, траекторию летящего камня, брошенного параллельно земле, наблюдатель измеряет в разные моменты времени расстояния от начала О до летящего камня М. В результате этого эксперимента наблюдатель получает набор расстояний r в каждый момент времени.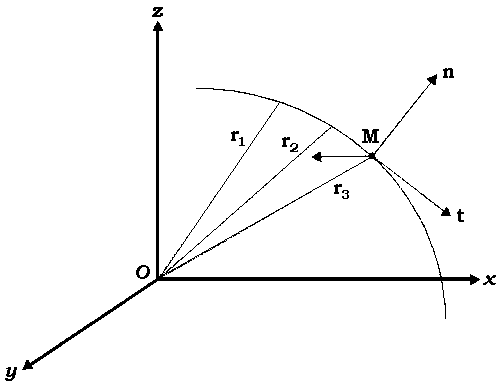
Рис. 1. Траектория камня, брошенного горизонтально поверхности земли. Наблюдатель измеряет расстояние r до камня в различные моменты времени t. Полученное множество относительных координат двух систем отсчёта содержит всю информацию о движении камня.
Анализируя полученные данные, он обнаруживает, что траектория камня описывается в данной системе наблюдения уравнением параболы.
Всякая реальная система отсчета связана с телом отсчета, в качестве которого может быть выбран любой физический объект - твердое тело, элементарная частица, волна света и т.д. Часто систему отсчета связывают со стенами лаборатории, в которой идет эксперимент. В нашем конкретном случае одна система отсчета связана с поверхностью Земли, а другая с брошенным камнем. Поэтому данные наблюдателя представляют собой множество относительных координат двух систем отсчета. Это все что мы имеем в любом физическом эксперименте!
И. Кеплер, измеряя положение планет в различные моменты времени при движении их вокруг Солнца, обнаружил, что они движутся по эллипсам. Он работал со множеством относительных координат двух систем отсчета, одна из которых была связана с Солнцем, а другая с планетой. Оказывается, что множество относительных координат содержит всю информацию о гравитационном взаимодействии планеты и Солнца.
И. Ньютон догадался (наверное, в тот момент, когда яблоко упало ему на голову), что Земля притягивает массивные предметы с силой, вид которой можно определить, анализируя множество относительных координат падающего предмета и системы отсчета, связанной с Землей. Однако первоначально И. Ньютон исследовал движение планет, Луны и спутников Юпитера и установил, что их движение происходит под действием силы, величина которой пропорциональна произведению масс планет и обратно пропорциональна квадрату расстояния между ними.
Предположим, что мы изучаем движение заряженной частицы в электромагнитном поле. Опять вводятся две системы отсчета, одна из которых связана с лабораторией, а другая с заряженной частицей. Измеряя относительные координаты двух этих систем отсчета в различные моменты времени, мы получаем множество относительных координат, содержащее всю информацию об электромагнитном взаимодействии поля и частицы. Множества относительных координат, полученные в различных опытах, физики называют пространством событий, поскольку каждая точка этого пространства описывает некоторое элементарное событие. Таким образом, изучая гравитационные, электромагнитные, ядерные или какие-либо другие физические взаимодействия, мы в самой основе имеем дело с пространством событий изучаемого явления.
Из наших рассуждений следуют, по крайней мере, два вывода:
1. Любой физический эксперимент прямым или косвенным образом сводится к измерению относительных координат различных систем отсчета.
2. Физика - это теория относительности, изучающая природу посредством анализа пространства событий.
Исследуя пространство событий какого-либо явления, физик, создавая теорию явления, может использовать два крайних подхода:
а) либо, на основе анализа пространства событий, попытаться угадать уравнения, которые описывают явление, так, как это сделал Ньютон при создании своей теории гравитации (индуктивный подход);
б) либо проанализировать общие геометрические свойства пространства событий и получить физические уравнения из этого анализа, так, как это сделал Эйнштейн при создании общей теории относительности (дедуктивный подход).
Уравнения теории физического вакуума были получены дедуктивным путем. Для этого был выбран наиболее общий класс систем отсчета, который известен в настоящее время в физике, а затем исследованы геометрические свойства соответствующего пространства событий.
В настоящее время в физике известно пять классов систем отсчета:
1) инерциальные, которые движутся друг относительно друга с постоянной скоростью и без вращения;
2) ускоренные локально инерциальные первого рода, которые движутся ускоренно друг относительно друга без вращения, но локально ничем не отличаются от инерциальных систем (например, система отсчета, связанная со свободно падающим лифтом);
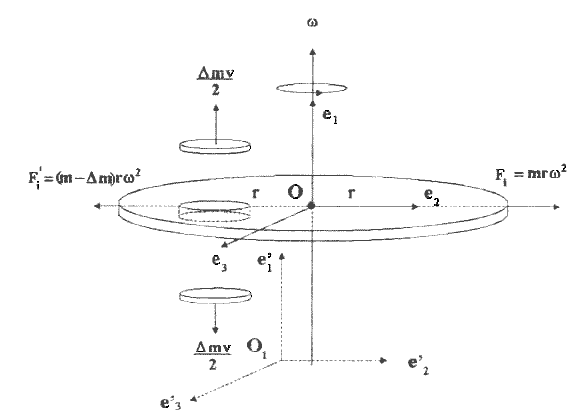
3) ускоренные локально инерциальные второго рода, которые движутся ускоренно относительно друг друга с вращением, но локально ничем не отличаются от инерциальных систем (например, система отсчета, связанная с центром масс однородного вращающегося диска);
4) ускоренные локально неинерциалъные (например, система отсчета, связанная с ускоряемой ракетными двигателями ракетой);
5) ускоренные конформные (такие системы связаны с физическими объектами, меняющими свои физические характеристики - массу, заряд и т. д. с течением времени).
Для каждого класса систем отсчета существует собственное, присущее только этому классу, пространство событий. Зная геометрические свойства пространства событий, можно найти, например, уравнения движения одной системы отсчета относительно другой. Поскольку система отсчета связана с каким-либо физическим телом, то мы сразу находим уравнения движения данного тела. Ясно, что ускоренное движение систем отсчета вызвано физическим взаимодействием тела отсчета с полем, в котором оно движется. Поэтому анализ пространства событий в этом случае позволяет найти не только уравнения движения тел отсчета, но и получить уравнения поля, под действием которого движется тело отсчета.
т движется ускоренно (вместе с кораблем) под действием гравитационной силы.
Понятие о системе отсчёта. Траектория тела в системе отсчёта. Тело отсчёта и его связь с системой отсчёта. Физический эксперимент как множество относительных координат двух систем отсчёта. Примеры экспериментов. Пространство событий. Физика как теория относительности, построенная на анализе пространства событий. Классы систем отсчёта: инерциальные, ускоренные локально инерциальные первого рода, ускоренные локально инерциальные второго рода, ускоренные локально неинерциальные, ускоренные конформные. Примеры систем отсчёта.
Относительность энергии равномерного движения.
Что такое абсолютная и относительная величина в физическом понимании? Мы будем говорить, что некоторая физическая величина относительна, если её можно обратить в нуль (хотя бы локально) с помощью каких-либо преобразований, имеющих физический смысл. Соответственно, если этого сделать нельзя, то физическая величина является абсолютной. Наблюдая, как Солнце восходит на Востоке и заходит на Западе, Аристотель и Птолемей пришли к выводу, что Земля находится в абсолютном покое, а Солнце и звезды вращаются вокруг неё. Однако более точные исследования астрономов показали, что Земля движется вокруг Солнца, а Солнце, в свою очередь, движется относительно звезд. Оказалось, что абсолютно покоящихся систем отсчета в природе не существует. Все находится в относительном движении.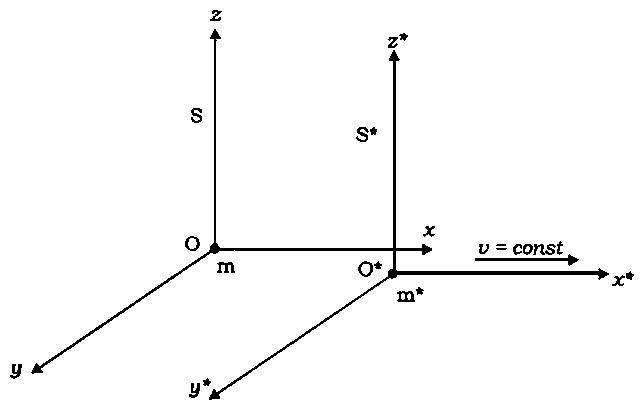
Рис. 2. Система отсчета S связана с массой m. Система отсчета S* связана с массой m*. Масса m* движется относительно массы m с постоянной скоростью v.
Выберем две системы отсчета, одна из которых S связана с массой m, а другая S* с массой m*. Предположим, что физик расположен в системе отсчета S и измеряет координаты до системы S*. Пусть система отсчета S* движется относительно системы S с постоянной скоростью v без вращения. По определению такая система отсчета является инерциальной. Понятно, что скорость тела отсчета m*, с которым связана система S*, также постоянна и равна v. В результате измерений физик получит множество относительных координат систем отсчета S и S* . Исследуя это множество он обнаружит, что:
а) трехмерная геометрия этого множества евклидова;
б) траектории тел отсчета представляют собой прямые линии;
в) кинетическая энергия тел отсчета является величиной относительной. Действительно, кинетическая энергия массы m*, записанная в координатах системы S равна половине произведения этой массы на квадрат скорости v. Перейдем теперь из системы S в систему S*, где масса m*, покоится (v = 0). В механике Ньютона такие переходы, совершаются с помощью координатных преобразований Галилея-Ньютона. В результате исследователь обнаружит, что кинетическая энергия тела m* в системе S* равна нулю. Этот результат как раз и доказывает, что кинетическая энергия инерциально движущихся тел относительна.
В геометрии существует понятие геодезической линии. Это линия соответствует кратчайшему расстоянию между двумя точками в данной геометрии. В геометрии Евклида геодезической (в дальнейшем слово линия мы будем опускать) является прямая. Поэтому уравнения движения тел отсчета надо записать в таком виде, чтобы их решения приводили к прямолинейным траекториям тел. Из механики Ньютона нам известно, что уравнения движения в этом случае запишутся в виде равенства нулю произведения массы тела на его ускорение. Это уравнения движения свободных тел. Но такого в природе не бывает! Все тела отсчета обладают массой и, следовательно, гравитационным взаимодействием. Конечно, это взаимодействие очень мало и в большинстве случаев им можно пренебречь (так обычно и поступают физики). Следовательно, понятие инерциальной системы отсчета является идеализированным. Исследуя пространство событий этих систем, мы получаем тривиальные уравнения движения и никаких уравнений поля. В этом смысле плоское пространство Евклида, образованное множеством относительных координат инерциальных систем отсчета, соответствует «абсолютной пустоте», так, как будто массы (и другие физические характеристики) тел отсчета устремились к нулю.
Абсолютная и относительная физическая величина. Примеры относительных физических величин. Понятие геодезической линии. Идеализация инерциальной системы отсчёта. Пространство Евклида как "абсолютная пустота"
Четырехмерное пространство событий и относительность времени.
Пространство событий инерциальных систем отсчета механики Ньютона трехмерно и использует три пространственных координаты х, у и z. При движении систем отсчета эти координаты зависят от времени t, которое выступает в механике Ньютона как абсолютная величина. Представления о трехмерности пространства сохранялись в физике до тех пор, пока не начались эксперименты, связанные с распространением света. Было установлено, что свет распространяется со скоростью с = 300000 км/сек.
При таких скоростях материи (или близких к ним, но меньших чем с) пространство событий становится четырехмерным, при этом время, умноженное на скорость света с образует четвертую координату Х0 = ct дополнительную к трем координатам х, у и z. В результате механику Ньютона заменила более совершенная релятивистская механика Эйнштейна-Лоренца. Геометрия пространства событий такой механики наделено структурой псевдоевклидовой геометрии. Это плоская геометрия, геодезические которой представляют собой четырехмерные прямые линии. По этим линиям движутся тела отсчета четырехмерных инерциальных систем. Название псевдоевклидова геометрия связано с тем, что четвертая координата х0 = ct выступает мнимой координатой по отношению к пространственным координатам х, у и z. Понятно, что четырехмерная инерциальная система отсчета является такой же идеализацией, как и трехмерная, поскольку, все тела отсчета хоть в какой-то степени взаимодействуют между собой.
Из анализа уравнений релятивистской механики (т.е. механики больших скоростей) вытекают удивительные следствия.
Во-первых, покоящееся тело отсчета обладает энергией покоя, равной произведению массы покоя m на квадрат скорости света: Е = mc2.
Во-вторых, масса тела зависит от скорости движения и стремится к бесконечно большой величине при приближении скорости тела к скорости света.
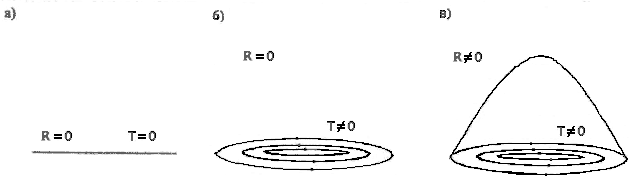
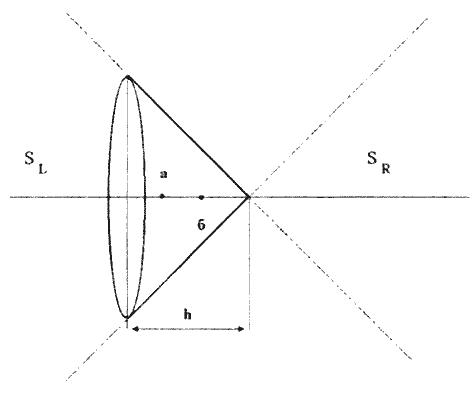
В третьих, всякое ускоренное поступательное движение в четырехмерном пространстве представляется как вращение в плоскостях, образованных осью времени ct и координатными осями х, у и z . На рис. 3 представлена одна из плоскостей, а именно, плоскость ct - х. На этой плоскости прямые, расположенные под углом к осям х и ct, представляют собой образующие светового конуса, по которым движется свет, естественно со скоростью света. Все тела отсчета, масса покоя которых m0 отлична от нуля, движутся внутри светового конуса, т.е. внутри сектора где расположена гиперболическая кривая.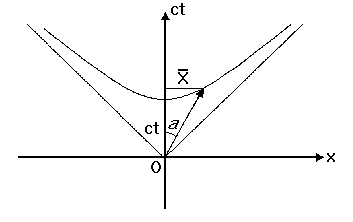
Рис.3. Плоскость ct-x, на которой изображены направляющие светового конуса будущего (t>0). Нерелятивисткая скорость движения вдоль оси Х вычисляется из прямоугольного треугольника через тангенс угла по следующей формуле v = x/t = ctga с.
Из рисунка видно, что скорость движения v = x/t вдоль оси х определяется через тангенс угла a, а изменение скорости сводится к вращению в плоскости ct - х.
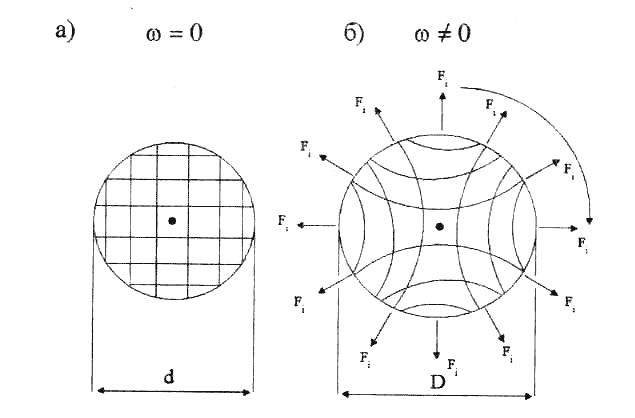
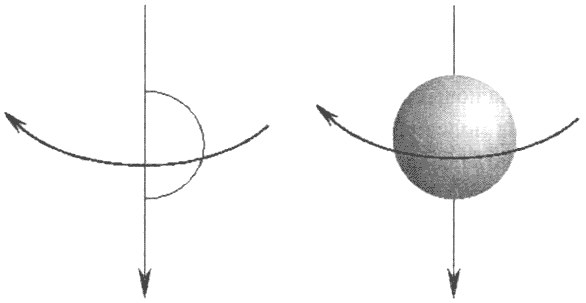
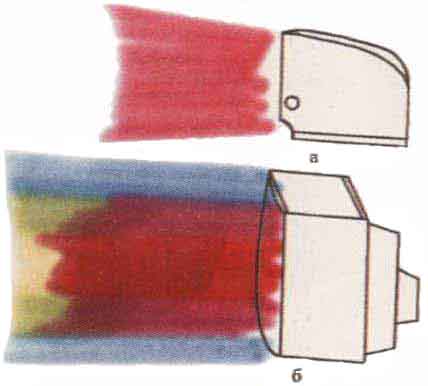
В четвертых, длина L0 любого объекта зависит от скорости и уменьшается с увеличением его скорости. При скорости v = с длина вдоль направления движения обращается в ноль. Например, наблюдатель, который следит за движущимся с большой скоростью шаром, увидит вместо круглого шара сплюснутый в направлении движения диск.
В пятых, время в четырехмерном пространстве становится величиной относительной и течет по-разному, в зависимости от скорости движения системы отсчета. Если астронавты в полете к далеким звездам будут двигаться в космическом корабле со скоростью, близкой к скорости света, то их время будет течь медленнее, чем на Земле.
Этот странный с житейской точки зрения вывод был неоднократно проверен экспериментально. Были измерены времена жизни неустойчивых (распадающихся на части) элементарных частиц в зависимости от скорости их движения. Оказалось, что чем ближе скорость частицы к скорости света, тем больше времени она живет.
Подобно плоской геометрии Евклида, псевдоевклидова геометрия приводит к тривиальным уравнениям движения тел отсчета (вспомним, что это уравнения движения свободных тел) и, соответственно, к отсутствию каких-либо уравнений поля. Можно сказать, что псевдоевклидова геометрия представляет собой четырехмерную модель «абсолютного вакуума». Эта модель соответствует реальности в пределе, когда массы тел отсчета стремятся к нулю.
Пространство событий инерциальной системы отсчёта в механике Ньютона. Механика Эйнштейна-Лоренца и её геометрия. Следствия уравнений релятивистской механики. Непостоянство массы и геометрических размеров тела. Энергия покоя. Псевдоевклидова геометрия как модель "абсолютного вакуума".
Относительность сил и полей в теории гравитации Эйнштейна.
До сих пор мы рассматривали пространство событий инерциальных систем отсчета. Сначала это были инерциальные системе механики Ньютона, которые движутся прямолинейно и равномерно без вращения относительно друг друга.
Пространство событий таких систем отсчета трехмерно и обладает геометрией Евклида. Затем, мы рассмотрели пространство событий инерциальных систем отсчета, которые движутся со скоростями, близкими к скорости света. В этом случае геометрия пространства событий оказалась четырехмерной, псевдоевклидовой. Обе эти геометрии описывают пустоту или абсолютный вакуум, где нет никакой материи или вообще чего-либо.
Перейдем теперь к описанию ускоренных систем отсчета, в частности к локально инерциальным системам без вращения. Что это за системы отсчета?
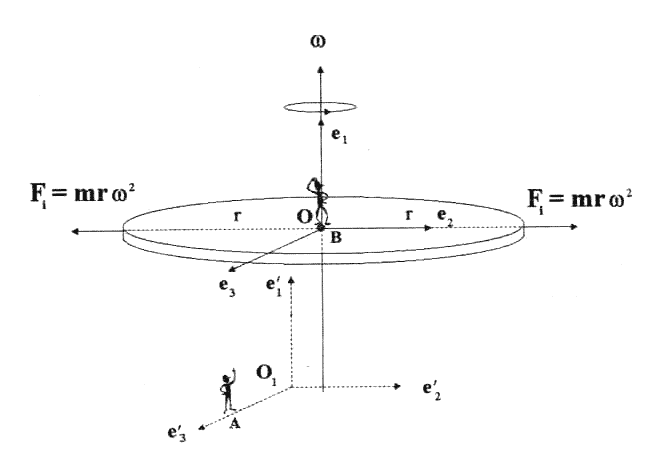
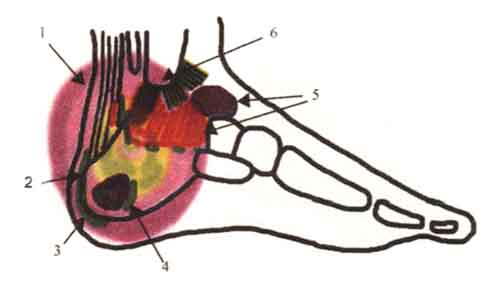
Представим себе космический корабль, который движется вокруг Земли по стационарной орбите без собственного вращения. В корабле находится космонавт в состоянии невесомости (см. рис. 4). Мы все это видели по телетрансляциям с борта космического корабля. Наблюдатель А находится на Земле и, измеряя координаты космонавта в своей системе отсчета, обнаруживает, что он движется под действием гравитационной силы Fg. Если масса космонавта m, то для наблюдателя А его уравнения движения запишутся как mа = Fg, где а - ускорение космонавта относительно наблюдателя А. Одним словом, наблюдатель видит, что космонавт движется ускоренно (вместе с кораблем) под действием гравитационной силы.
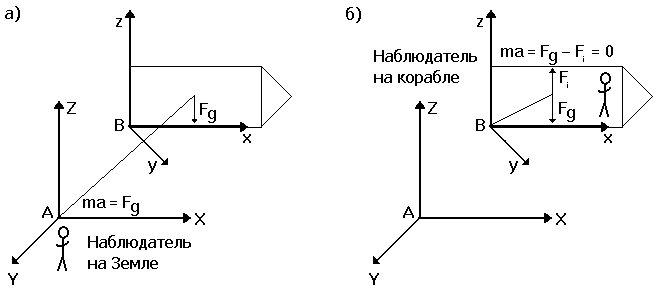
Рис. 4. Ускоренная система отсчета В, связана с космическим кораблем. Корабль совершает свободный полет на стационарной орбите и движется без собственного вращения. Система отсчета А находится на Земле. Наблюдатели А и В измеряют координаты до космонавта, находясь каждый в своей системе отсчета, и получают разные уравнения движения космонавта.
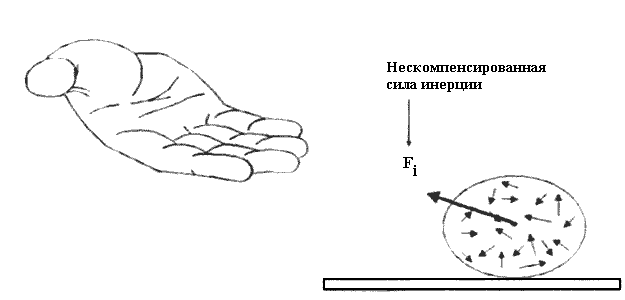
Предположим теперь, что на корабле находится наблюдатель В и измеряет координаты космонавта относительно системы отсчета, связанной с космическим кораблем. Он заметит, что внутри корабля космонавт либо покоится относительно стенок корабля, либо будет двигаться прямолинейно и равномерно, так, как будто никакие силы на космонавта не действуют. На самом же деле на космонавта действуют две силы, которые компенсируют друг друга. Одна из них все та же гравитационная сила Fg, а другая Fi - сила инерции (см. рис. 4). Физикам известно, что в ускоренных системах отсчета действуют силы инерции. Например, когда вы катаетесь на карусели, на вас действует центробежная сила инерции, которая пытается сбросить вас с карусели. Вращение представляет собой ускоренное движение.
Теперь понятно, как определить ускоренную локально инерциальную систему отсчета первого рода. Это такая ускоренная система, в которой внешняя сила, действующая на тело отсчета, скомпенсирована силой инерции. В нашем случае внешней силой оказалась гравитационная сила Fg. Именно такие системы отсчета использовал А. Эйнштейн при построении теории гравитационного поля.
Итак, мы показали, что в теории Эйнштейна гравитационные поля и силы носят относительный характер, поскольку могут быть обращены в нуль (правда, только локально) путем перехода в ускоренную локально инерциальную систему отсчета. Далее, А. Эйнштейну удалось установить, что относительные координаты ускоренных локально инерциальных систем образуют пространство событий, наделенное геометрией Римана. В отличие от плоской геометрии Евклида (или плоской псевдоевклидовой геометрии) эта геометрия обладает кривизной. Оказалось, что кривизна геометрии Римана содержит всю необходимую информацию о гравитационных полях и взаимодействиях. Вспомним теперь высказывания Клиффорда о том, что в мире ничего не происходит, кроме изменения кривизны пространства. А. Эйнштейну удалось показать это для гравитационных взаимодействий!
Рис. 5. Отклонение луча света вблизи поверхности Солнца.
Используя математические знания о различных геометрических объектах геометрии Римана, можно заранее предсказать результат любого гравитационного эксперимента. Например, уравнения движения тела отсчета, с которым связана ускоренная локально инерциальная система, в теории гравитации Эйнштейна описывается уравнениями геодезических. Эти уравнения были известны математикам задолго до теории Эйнштейна. Великий ученый использовал эти уравнения для теоретических расчетов, заранее зная, что теоретические выводы будут подтверждены экспериментом. Он предсказал, что луч света от далекой звезды, проходящий вблизи Солнца, будет искривляться под действием гравитационного поля (см. рис.5).
В последствии эксперименты, проведенные астрономами, количественно подтвердили предсказанный А. Эйнштейном угол отклонения луча. Были и другие предсказания теории, получившие количественные подтверждение на опыте.
Описание локально инерциальных систем отсчёта. Определение ускоренной локально инерциальной системы отсчёта первого рода. Теория гравитации Эйнштейна и пространство событий геометрии Римана. Эксперименты, подтверждающие теорию гравитации Эйнштейна.
Вакуум Эйнштейна.
После многолетних поисков А. Эйнштейн после дискуссии с немецким математиком Д. Гильбертом находит в 1915 году знаменитые уравнения Эйнштейна, которые описывают гравитационные поля через кривизну пространства событий. Согласно этим уравнениям, массивное тело искривляет пространство-время вокруг себя. В его теории имеется две реальности: пространство-время и материя. Материя выступает на фоне пространства-времени, искривляя его. Если материю убрать, что пространство становится плоским (псевдоевклидовым). Таким образом, пространство-время наделяется упругими свойствами, которые проявляются через искривление его геометрии. Наглядно смоделировать физический процесс отклонения луча света, показанный на рис. 5, можно следующим образом. Представим себе область трехмерного пространства, заполненного прозрачной однородной резиной. Пропуская луч света по различным направлениям внутри резины, мы увидим, что он распространяется всегда по прямой линии. Это модель плоского пространства или «абсолютного вакуума».
Поместим внутрь резины шарик из какого-либо твердого материала. В результате вблизи поверхности шарика возникнут неоднородности из-за вытеснения шариком части объема резины. Если теперь пропустить луч света вблизи поверхности шарика, то он будет распространяется по некоторой кривой из-за неоднородной плотности вблизи поверхности. В данном случае неоднородный кусок прозрачной резины моделирует искривленное пространство или возбужденный вакуум.
Можно теперь утверждать, что согласно теории Эйнштейна физический вакуум это пустое (без материи) пространство-время, обладающее упругими свойствами. Эти свойства проявляются тогда, когда в пустое пространство помещается некая масса. Более того, в теории имеются так называемые вакуумные уравнения Эйнштейна, которые описывают гравитационные поля вне материи, т.е. в чистом виде упругие свойства пустого пространства-времени. Вакуумные уравнения Эйнштейна являются чисто геометрическими и не содержат никаких физических констант. Это так и должно быть, поскольку вакуум не может характеризоваться чем-либо конкретным. Если вакуум наделить какими-нибудь конкретными физическими константами, то это будет уже что-то рожденное из вакуума.
Следствия из уравнений Эйнштейна. Упругие свойства пространства-времени. Физический вакуум в понимании Эйнштейна и его вакуумные уравнения.
Вакуум Дирака.
Обратим внимание на очень важный момент. При построении теории гравитации А. Эйнштейн не был ориентирован на эксперимент. Вся содержательная часть теории связана с геометрическими свойствами пространства событий относительных координат ускоренных локально инерциальных систем отсчета первого рода. Достаточно знать, что пространство событий таких систем наделено структурой геометрии Римана, как уже из этого факта следуют уравнения движения массы в произвольном гравитационном поле - уравнения геодезических! Теории такого класса можно назвать дедуктивными.
Большинство физических теорий строится на основе обобщения экспериментальных данных частного характера. Такие теории относятся к классу индуктивных. Примером индуктивной теории является механика Ньютона, термодинамика, электродинамика, квантовая механика и ее наиболее развитая часть - квантовая электродинамика. На сегодняшний день квантовая электродинамика, основателем которой по праву считается П. Дирак, являет собой пример наиболее разработанной физической теории. Теоретические выводы, следующие из ее уравнений, совпадают с результатами опыта с высокой степенью точности (с точностью до величин порядка 10-7). Тем не менее, не опыт является истиной. Это всего лишь критерий истины. Дело в том, что анализ уравнений квантовой электродинамики позволяет выяснить ряд трудностей. Они приводят к противоречивым выводам и указывают на незаконченность уравнений квантовой электродинамики. П. Дирак это прекрасно понимал и с горечью замечал, что «правильный вывод состоит в том, что основные уравнения неверны». Если бы эти слова произнес не П. Дирак, а какой-нибудь другой даже очень авторитетный теоретик, все остальные физики подумали бы, что он сумасшедший!
Уравнения, которые открыл Дирак, показывают, что в природе существуют частицы с положительной энергией - электроны и античастицы - позитроны, энергия которых отрицательна. Они рождаются парами электрон-позитрон из физического вакуума. Сам же вакуум представляет собой некоторое латентное (скрытое) состояние электронов и позитронов. В среднем физический вакуум не имеет ни массы, ни заряда, ни каких-либо других физических характеристик. Однако в малых пространственных областях (порядка 10-33) вакуума значения физических характеристик могут стать отличными от нуля - на малых расстояниях вакуум спонтанно флуктуирует. В вакууме постоянно происходят процессы рождения и уничтожения частиц и античастиц разного сорта. Образно говоря, в малых пространственно-временных областях вакуум похож на «кипящий бульон», состоящий из элементарных частиц. Поэтому в квантовой теории возникло представление о физическом вакууме как о «квантовой жидкости», находящейся в вечном движении. Такая жидкость описывается уравнениями квантовой гидродинамики и, естественно, обладает упругими свойствами подобно вакууму Эйнштейна. Для физиков важным оказался вопрос, как объединить уравнения, которые описывают вакуум Эйнштейна и вакуум Дирака с тем, чтобы иметь более правильное представление о нем. В этом вопросе мнения физиков резко разделились.
Индуктивные и дедуктивные теории, примеры. Проблемы уравнений квантовой электродинамики. Физический вакуум как "квантовая жидкость".
Завещание Эйнштейна будущей физике.
К сожалению надо отметить, что за последние сорок лет произошла демократизация физики в худшем смысле этого слова. В процессе принятия важных для развития физики решений принимают участие большие коллективы людей или люди далекие от стратегического мышления. По всем основным вопросам развития существует общественное мнение, которое висит тяжелыми кандалами на всякой оригинальной мысли. Даже А. Эйнштейн, ученый, внесший вклад в развитие трех современных теорий - квантовой теории, специальной и общей теории относительности, подвергался при жизни обструкции. Его точка зрения на физическое содержание современной квантовой механики не принималась большинством современников. Еще Декарт отмечал, что при решении очень сложных вопросов большинство, как правило, ошибается.
С этим можно было бы смириться, если бы не колоссальные материальные потери, которые несет общество за неверно принятые учеными решения. К таким решениям можно причислить проблему управляемой термоядерной реакции при отсутствии фундаментальной теории ядерных сил, строительство суперускорителей и планирование экспериментов в отсутствии теории элементарных частиц и т. д. В таких условиях значение стратегических работ, оценить которые может ограниченное число ученых, бесценно.
Всех исследователей, которые занимаются теоретической физикой, можно разделить на три большие группы: стратеги, тактики и оперативники.
Стратеги создают фундаментальные теории, которые определяют развитие физики на десятки, а то и сотни лет. Фундаментальные теории подразумевают открытие принципиально новых физических уравнений. Эти уравнения основаны на новых физических принципах общего характера (механика Ньютона, специальная и общая теория относительности Эйнштейна). Теоретические предсказания фундаментальных теорий абсолютно точно подтверждаются на опыте в той области, где уравнения и принципы теории справедливы. К теоретикам-стратегам можно отнести только двух ученых - И. Ньютона и А. Эйнштейна.
Тактики детально разрабатывают отдельные фрагменты стратегической работы. В их среде находятся ученые, которые в состоянии оценить еще не признанную научным сообществом стратегическую работу. К теоретикам-тактикам относятся такие исследователи, как Дж. Максвелл, М. Планк, Э. Шредингер, П. Дирак, В. Паули и многие другие известные ученые.
Большинство известных физиков-теоретиков занимается оперативными работами. Это, прежде всего, создание феноменологических (описательных) теорий, обладающих ограниченной предсказательной силой. К таким теориям относятся теории сильных и слабых взаимодействий или различные супер и гранд теории. К оперативным работам относятся решения конкретных задач, поставленных стратегической или тактической физикой. К оперативной работе относится так же разработка новых математических методов для решения уже известных фундаментальных уравнений. Те из теоретиков-оперативников, которые обладают хорошими организационными способностями, создают собственные научные школы и пишут учебники по теоретической физике. К известным теоретикам-оперативникам можно отнести А. Зоммерфельда, Л. Ландау, Д. Швингер, М. Гелл-Манн, А. Салам, С. Вайнберг, С. Глэшоу и др. Как правило, оперативники прекрасно владеют математическим аппаратом и имеют энциклопедические знания в области физики. Они быстро завоевывают признание научного сообщества, и именно они определяют «общественное мнение» по тому или иному сложному физическому вопросу, сводя его к математическим проблемам.
Однако в стратегической физике не было, и нет проблем математических. Есть только проблемы физические. Это хорошо понимал А.Эйнштейн.
После завершения работы по созданию теории гравитации, в которой гравитационные поля имеют относительную природу, А. Эйнштейн приступил к поиску уравнений единой теории поля. Он полагал, что физика должна быть единой и что существуют уравнения, которые описывают все явления, наблюдаемые в природе.
Программа построения единой теории поля является стратегической проблемой физики. А. Эйнштейн разделил ее на две части:
а) программа минимум, предполагающая открытие таких уравнений электродинамики, которые приводят к геометрическому описанию электромагнитных взаимодействий, подобно тому, как это имеет место в теории гравитации Эйнштейна;
б) программа максимум, предполагающая открытие уравнений геометризированной квантовой теории путем дальнейшего совершенствования теории относительности.
Далее будет показано, что развитие именно этих программ приводит нас к теории физического вакуума, новому мировоззрению и новым технологиям.
Проблема "демократизации физики". Три основные группы исследователей: стратеги, тактики и оперативники. Программа Эйнштейна по построению единой теории поля.
Относительность электромагнитного поля в геометризированной электродинамике.
Науке известны две теории гравитационного поля - Ньютона и Эйнштейна. Теория Ньютона была построена индуктивным путем на основе анализа большого числа экспериментальных данных. Наоборот, теория гравитации Эйнштейна не опиралась на экспериментальные данные и была построена на основе дедукции. Эйнштейну достаточно было предположить, что пространство относительных координат ускоренных локально инерциальных систем отсчета первого рода (свободно падающих лифтов) наделено геометрией Римана, как из этого факта уже можно было получить уравнения движения, а затем и уравнения поля его теории.
Ничто не запрещает нам сделать то же самое при геометризации уравнений электромагнитного поля, реализуя эйнштейновскую программу минимум по построению единой теории поля. Для этого, сделаем предположение, что в электродинамике существуют ускоренные локально инерциальные системы отсчета первого рода, связанные с заряженными частицами. Это означает, что в электромагнитных явлениях существуют такие ситуации, когда заряд движется ускоренно, но так, что локально в каждой точке траектории внешняя электромагнитная сила полностью скомпенсирована силой инерции. В результате такой заряд в каждой точке криволинейной траектории будет локально двигаться инерциально, т.е. равномерно и прямолинейно без вращения. Более того, из-за инерциальности движения в каждой точке траектории заряд не будет излучать электромагнитных волн как локально, так и вдоль всей криволинейной траектории, несмотря на то, что его движение является ускоренным!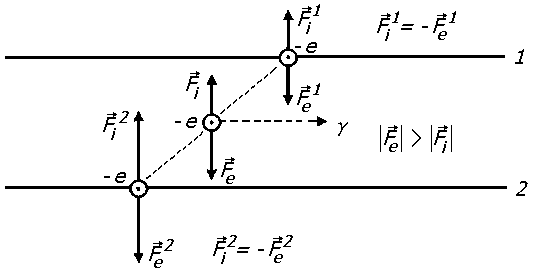
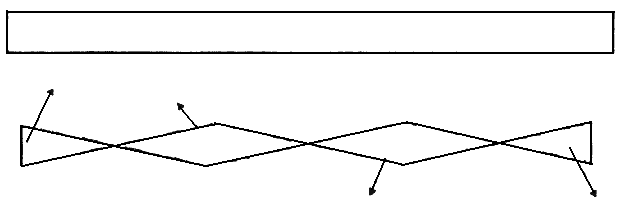
Рис. 6. Переход электрона со стационарного уровня 1 на стационарный уровень 2. На уровнях 1 и 2 электромагнитная сила Fe скомпенсирована силой инерции Fi. Электромагнитное излучение появляется, когда [Fe] > [Fi].
Этот парадоксальный с первого взгляда вывод имеет, тем не менее, экспериментальное подтверждение. Действительно, из анализа атомных спектров следует, что при движении электрона вокруг ядра у электрона существуют устойчивые орбиты, по которым электрон движется ускоренно, но без излучения. Наблюдаемая устойчивость атомных орбит электрона была возведена Н. Бором в ранг физического принципа при построении квантовой теории атома. Под давлением экспериментальных данных ученый вводит постулат стационарности электронных орбит в атоме. Постулат Бора становится лишним, если связать с электроном в атоме ускоренную локально инерциальную систему отсчета первого рода (см. рис. 6).Так же как в теории гравитации Эйнштейна в новой электродинамике пространство событий относительных координат ускоренных систем отсчета, связанных с зарядами, наделено структурой геометрии Римана. Поэтому уравнения движения заряда в геометризированной электродинамике совпадают с уравнениями геодезических пространства Римана. В эти уравнения входят электромагнитные поля, которые преобразованием координат можно обратить в нуль локально. Иными словами, электромагнитное поле в геометризированной электродинамике имеет относительную природу. Поскольку электромагнитные силы порождены электромагнитными полями, то они так же относительны. На рис. 7 схематически показано как координатные преобразования делают относительными электромагнитные силы в геометризированной электродинамике.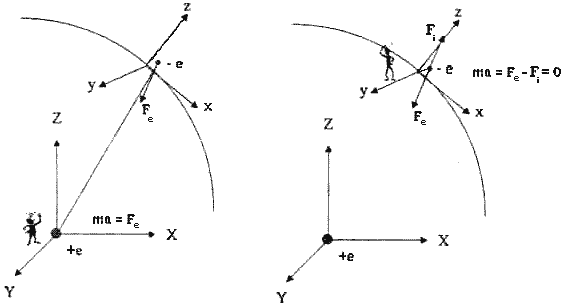
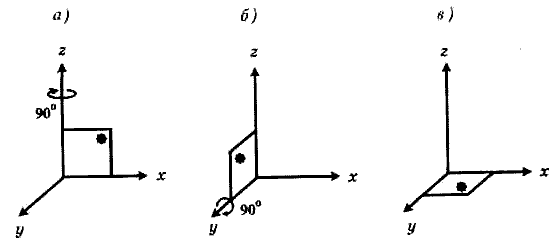
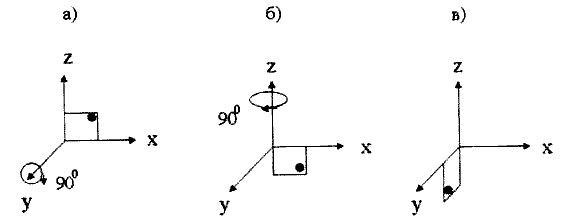
Рис. 7. Электрон - е движется по стационарной орбите вокруг ядра атома с зарядом +е. На левом рисунке наблюдатель видит движение электрона под действием внешней силы Fе На правом рисунке наблюдатель обнаружит в локально инерциальной системе прямолинейное и равномерное движение электрона.
На рисунке 7а наблюдатель находится в инерциальной системе отсчета, связанной с атомным ядром, имеющим заряд +е. Измеряя относительные координаты своей системы отсчета и ускоренной системы, связанной с электроном -е массы m он видит, что электрон движется с ускорением под действием силы Fe.
Она порождена электромагнитным полем ядра. Используя преобразования координат, наблюдатель может переместиться в ускоренную систему отсчета (см. рис. 7в). На рисунке 7в он находится в ускоренной локально инерциальной системе отсчета вблизи электрона. В этой системе отсчета он видит, что локально электрон либо покоится, либо движется прямолинейно и равномерно без вращения, поскольку локально внешняя сила Fe скомпенсирована силой инерции Fi. С точки зрения локального наблюдателя действие на электрон какого-либо поля отсутствует, что и указывает на относительность электромагнитного поля.
Из наших рассуждений можно прийти к выводу, что в геометризированной электродинамике возможно ускоренное движение по «инерции». Для этого заряженной частице достаточно двигаться согласно уравнениям геодезических пространства Римана. Причем это пространство должно быть образовано множеством относительных координат ускоренных локально инерциальных систем отсчета, связанных с зарядами. Поэтому в геометризированной электродинамике существование стационарных орбит электронов в поле ядра (квантовый принцип Бора) есть следствие ускоренного движения зарядов по инерции.
Этот вывод подтверждает догадки А. Эйнштейна о возможности найти более совершенную квантовую теорию путем расширения принципа относительности. В самом деле, появление стационарных орбит у электрона в геометризированной электродинамике обеспечено расширением специального принципа относительности электродинамики Максвелла-Лоренца-Эйнштейна до общего принципа относительности.